数据结构 | Welcome

数据结构复习（C语言）中国大学慕课（浙大：陈越、何钦铭教授）

打卡第一天

第一讲基本概念

1.1 什么是数据结构

写程序计算多项式在给定点x处的值

/**
*f(x)=a0+a1x+……+a(n-1)x^n-1+anx^n 
*/
#include<stdio.h>
#include<time.h>
#include<math.h>
#define MAXN 10
#define MAXK 1e7 /*被测函数最大重复调用次数*/ 
/*clock_t是clock()函数返回的变量类型*/
clock_t start,stop;
/*记录被测函数的运行时间，以秒为单位*/ 
double duration; 

double f1(int n, double a[], double x);
double f2(int n,double a[],double x);
int main(){
	int i;
	double a[MAXN];
	for(i=0;i<MAXN;i++){
		a[i] = (double)i;
	}
	/*不在测试范围内的准备工作写在clock()调用之前*/
	start = clock();/*开始计时*/ 
	for(i=0;i<MAXK;i++){
		f1(MAXN-1,a,1.1);
	}
	stop = clock();
	duration = ((double)(stop-start))/CLK_TCK/MAXK;
	/*其他不在测试范围的处理写在后面例如输出duration的值*/
	printf("tickets1 = %f\n",(double)(stop-start));
	printf("f1:%6.2e\n",duration); 
	/*不在测试范围内的准备工作写在clock()调用之前*/
	start = clock();/*开始计时*/ 
	for(i=0;i<MAXK;i++){
		f2(MAXN-1,a,1.1);
	}
	stop = clock();
	duration = ((double)(stop-start))/CLK_TCK/MAXK;
	/*其他不在测试范围的处理写在后面例如输出duration的值*/
	printf("tickets2 = %f\n",(double)(stop-start));
	printf("f2:%6.2e\n",duration); 
}


/*普通算法*/ 
double f1(int n, double a[], double x){
	int i;
	double p = a[0];
	for(i=1;i<=n;i++){
		p+=(a[i]*pow(x,i));
	}
	return p;
}
/*秦九韶算法*/ 
double f2(int n,double a[],double x){
	int i;
	double p = a[n];
	for(i=n;i>0;i--){
		p=a[i-1]+x*p;
	}
	return p;
}

tickets1 = 2112.000000
f1:2.11e-007
tickets2 = 287.000000
f2:2.87e-008

--------------------------------
Process exited after 5.22 seconds with return value 13
请按任意键继续. . .

相差了一个数量级，秦九韶完胜！！！

什么是数据结构？
- 数据对象在计算机中的组织方式
- 数据对象必定与一系列加在其上的操作相关联
- 完成这些操作所用的方法就是算法
- 抽象数据类型（只描述对象集合相关操作集“是什么”，并不涉及“如何做到”的问题）
  - 数据类型
    - 数据对象集
    - 数据集合相关联的操作集
  - 抽象：描述数据类型的方法不依赖于具体实现
    - 与存放的机器无关
    - 与数据存储的物理结构无关
    - 与实现操作的算法和编程语言均无关

1.2 什么是算法

算法定义（Algorithm）
- 一个有限指令集
- 接受一些输入（有些情况下不需要输入）
- 产生输出
- 一定在有限步骤之后终止
- 每一条指令必须
  - 有充分明确的目标，不可以有歧义
  - 计算机能处理的范围之内
  - 描述应不依赖于任何一种就算及语言以及具体的实现手段
什么是好的算法？
- 空间复杂度S(n) —— 根据算法写成的程序在执行时 占用存储单元的长度。
  - 最好情况复杂度T_best(n)
  - 最坏情况复杂度T_worst(n)
  - 平均时间复杂度T_avg(n)
    
    T_best(n) < T_avg(n) < T_worst(n)
- 时间复杂度T(n) —— 根据算法写成的程序在执行时 耗费时间的长度。
复杂度的渐进表示法
- T(n) = O(f(n))表示存在常数C>0,n₀>0使得当n≥n₀时有T(n)≤C·f(n) ——> O(f(n))是T(n)的上界
- T(n) = Ω(g(n))表示存在常数C>0,n₀>0使得当n≥n₀时有T(n)≥C·g(n) ——> Ω(g(n))是T(n)的下界
- T(n) = Θ(h(n))表示同时有T(n)=O(h(n))和T(n)=Ω(h(n)) ——> Θ(h(n))既是T(n)的上界又是T(n)的下界
复杂度分析小窍门
- 若两端算法分别有复杂度T₁(n)=O(f₁(n))和T₂(n)=O(f₂(n))，则
  - T₁(n) + T₂(n) = max(O(f₁(n)),O(f₂(n)))
  - T₁(n) × T₂(n) = O(f₁(n)×f₂(n))
- 若T(n)是关于n的k阶多项式，那么T(n) = Θ(n^k)
- 一个for循环的时间复杂度等于循环次数乘以循环体的代码复杂度
- if-else结构的复杂度取决于if的条件判断复杂度和两个分支部分的复杂度，总体复杂度取三者中最大

1.3 最大子列和问题

给定N个整数的序列{A₁,A₂,…,A_N},求函数f(i,j) = max{0,∑A_k}的最大值。

算法1 O(n³)

int MaxSubSequm1(int A[], int N)
{
    int ThisSum, MaxSum = 0;
    int i, j, k;
    for (i = 0; i < N; i++)  {  // i 是子列左端的位置
        for (j = i; j < N; j++){ //j 是子列右端的位置
            ThisSum = 0;              
            for (k = i; k <= j; k++)   
                ThisSum += A[k];      
            if (ThisSum>MaxSum)  // 如果刚得到的子列和更大
                MaxSum = ThisSum; // 更新结果
 
        }
 
    }// 循环结束
    return MaxSum;

算法2 O(n²)

 
int MaxSubSequm1(int A[], int N)
{
    int ThisSum, MaxSum = 0;
    int i, j, k;
    for (i = 0; i < N; i++)  {  // i 是子列左端的位置
        for (j = i; j < N; j++){ //j 是子列右端的位置
            ThisSum +=A[j];               
                  // 对于相同i ,的不同j ,只要在j-1次循环的基础上累加1 项即可
 
            if (ThisSum>MaxSum)  // 如果刚得到的子列和更大
                MaxSum = ThisSum; // 更新结果
 
        }
 
    }// 循环结束
    return MaxSum;   
}

分而治之 O(nlog_n)

int Max3( int A, int B, int C )
{ /* 返回3个整数中的最大值，注计算机会自动把满足三目表达式的看做一个整体 */
    return A > B ? A > C ? A : C : B > C ? B : C;
}
   
int DivideAndConquer( int List[], int left, int right )
{ /* 分治法求List[left]到List[right]的最大子列和 */
    int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */
    int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/
   
    int LeftBorderSum, RightBorderSum;
    int center, i;
   
    if( left == right )  { /* 递归的终止条件，子列只有1个数字 */
        if( List[left] > 0 )  return List[left];
        else return 0;
    }
   
    /* 下面是"分"的过程 */
    center = ( left + right ) / 2; /* 找到中分点 */
    /* 递归求得两边子列的最大和，注：递归算法经过return会挑出当前递归，返回上一层递归 */
    MaxLeftSum = DivideAndConquer( List, left, center );
    MaxRightSum = DivideAndConquer( List, center+1, right );
   
    /* 下面求跨分界线的最大子列和 */
    MaxLeftBorderSum = 0; LeftBorderSum = 0;
    for( i=center; i>=left; i-- ) { /* 从中线向左扫描 */
        LeftBorderSum += List[i];
        if( LeftBorderSum > MaxLeftBorderSum )
            MaxLeftBorderSum = LeftBorderSum;
    } /* 左边扫描结束 */
   
    MaxRightBorderSum = 0; RightBorderSum = 0;
    for( i=center+1; i<=right; i++ ) { /* 从中线向右扫描 */
        RightBorderSum += List[i];
        if( RightBorderSum > MaxRightBorderSum )
            MaxRightBorderSum = RightBorderSum;
    } /* 右边扫描结束 */
   
    /* 下面返回"治"的结果 */
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}
   
int MaxSubseqSum3( int List[], int N )
{ /* 保持与前2种算法相同的函数接口 */
    return DivideAndConquer( List, 0, N-1 );
}

在线处理算法 O(n)

int MaxSubseqSum4(int A[], int N)
{
    int ThisSum, MaxSum;
    int i;
    ThisSum = MaxSum = 0; 
    for (i = 0; i < N; i++){ 
        ThisSum += A[i];//向右累加
        if (ThisSum>MaxSum)
            MaxSum = ThisSum; // 发现更大和则更新当前结果
        else if (ThisSum < 0)  // 如果当前子列和为负数
            ThisSum = 0; // 则不可能使后面部分和增大，抛弃之
    }
    return MaxSum;
}

第二讲线性结构

2.1 线性表及其实现

多项式表示
- 数据
- 链表
什么是线性表？

“线性表(Linear List)**”：有同类型数据元素构成有序序列**的线性结构
- 表中元素个数称为线性表的长度
- 线性表没有元素时，成为空表
- 表起始位置称表头，表结束位置成表尾
线性表的抽象数据类型描述
- 类型名称：线性表（List)
- 数据对象集：线性表是n(≥0)个元素构成的有序序列(a₁,a₂,…,a_n)
- 操作集：线性表L∈List，整数i表示位置，元素X∈ElementType，
- 线性表的基本操作主要有：
  - List MakeEmpty()：初始化一个空线性表L；
  - ElementType FindKth(int K,List L)：根据位序K，返回相应元素；
  - int Find(ElementType X,List L)：在线性表L中查找X的第一次出现位置；
  - void Insert(ElementType X, int i, List L)：在位序i前插入一个新元素X；
  - void Delete(int i,List L)：删除指定位序i的元素；
  - int Length(List L)：返回线性表L的长度n

线性表的顺序存储实现

利用数组的连续存储空间顺序存放线性表的各元素

#include<stdio.h>
#include<malloc.h>
#define MAXSIZE 100
typedef int ElementType;
typedef struct LNode *List;
struct LNode{
	ElementType Data[MAXSIZE];
	int Last;
};
//struct LNode L;
List PtrL;
/*初始化（建立空的顺序表）*/
//List MakeEmpty(){
//	PtrL = (List)malloc(sizeof(struct LNode));
//	PtrL->Last = -1;
//	return PtrL; 
//} 
/*按值查找O(n)*/
int Find(ElementType X, List PtrL){
	int i=0;
	while(i<=PtrL->Last&&PtrL->Data[i]!=X)
		i++;
	if(i>PtrL->Last)
		return -1;
	else return i;
}
/*按序查找*/
ElementType FindKth(int K,List PtrL){
	if(K<0||PtrL->Last<K){
		printf("不存在该元素");
		return;
	}
	return PtrL->Data[K];
} 
/*插入（第i个位置上插入一个值为X的新元素）O(n) */
int Insert(ElementType X,int i,List PtrL){
	int j;
	if(PtrL -> Last == MAXSIZE-1){
		printf("表满了");
		return; 
	}
	if(i<0||i>PtrL->Last+1){
		printf("位置不合法");
		return; 
	}
	for(j=PtrL->Last;j>=i;j--)
		PtrL->Data[j+1] = PtrL->Data[j];
	PtrL->Data[i] = X;
	PtrL->Last++;
	return;
}
/*删除O(n)*/
void Delete(int i,List PtrL){
	int j;
	if(i<0||i>PtrL->Last){
		printf("不存在第%d个元素",i); 
		return; 
	}
	for(j=i+1;j<=PtrL->Last;j++)
		PtrL->Data[j-1] = PtrL->Data[j];
		PtrL->Last--;
		return;
}
int main(){
	int i=0;
	PtrL = MakeEmpty();
	Insert(11,0,PtrL);
	printf("在线性表PtrL-Data[0]插入11\n");
	Insert(25,0,PtrL);
	printf("在线性表PtrL-Data[0]插入25\n");
	Insert(33,0,PtrL);
	printf("在线性表PtrL-Data[0]插入33\n");
	Insert(77,0,PtrL);
	printf("在线性表PtrL-Data[0]插入77\n");
	printf("此时的线性表为："); 
	for(i=0;i<PtrL->Last+1;i++)
		printf("%d ",PtrL->Data[i]);
	printf("\n");
	printf("查找值为11的下标是：%d\n",Find(11,PtrL));
	printf("下标为3的线性表的值是：%d\n",FindKth(3,PtrL));
	Delete(2,PtrL);
	printf("删除线性表中下标为2的元素\n");
	Delete(2,PtrL);
	printf("删除线性表中下标为2的元素\n");
	printf("此时的线性表为："); 
	for(i=0;i<PtrL->Last+1;i++)
		printf("%d ",PtrL->Data[i]);
	printf("\n"); 
	return 0;
}

在线性表PtrL-Data[0]插入11
在线性表PtrL-Data[0]插入25
在线性表PtrL-Data[0]插入33
在线性表PtrL-Data[0]插入77
此时的线性表为：77 33 25 11
查找值为11的下标是：3
下标为3的线性表的值是：11
删除线性表中下标为2的元素
删除线性表中下标为2的元素
此时的线性表为：77 33

--------------------------------
Process exited after 0.5634 seconds with return value 0
请按任意键继续. . .

线性表的链式存储实现

#include<stdio.h>
#include<malloc.h>
typedef int ElementType;
typedef struct LNode *List;
struct LNode{
	ElementType Data;
	List Next;
};
List PtrL;
/*初始化链表*/
List MakeEmpty(){
	List PtrL = (List)malloc(sizeof(struct LNode));
	PtrL = NULL;
	return PtrL;
}
/*求链表的长度*/
int Length(List PtrL){
	List L = PtrL;
	int i=0;
	while(L){
		L = L->Next;
		i++;
	}
	return i;
} 
/*按序查找*/
List FindKth(int K,List PtrL){
	List L = PtrL;
	int i=1;
	while(L&&i<K){
		L = L->Next;
		i++;
	}
	if(i==K){
		return L;
	}
	else{
		return NULL;
	}
}
/*按值查找*/
List Find(ElementType X,List PtrL){
	List L = PtrL;
	while(L&&X!=L->Data){
		L = L->Next;
	}
	return L;
}
/*插入*/
List Insert(ElementType X,int i,List PtrL){
	List L,P;
	if(i==1){
		L = (List)malloc(sizeof(struct LNode));
		L->Data = X;
		L->Next = PtrL;
		return L; 
	}
	P = FindKth(i-1,PtrL);
	if(!P){
		printf("结点不存在");
		return NULL; 
	}else{
		L = (List)malloc(sizeof(struct LNode));
		L->Data = X;
		L->Next = P->Next;
		P->Next = L;
		return PtrL;
	} 
}
/*删除*/
List Delete(int i,List PtrL){
	List L,P;
	if(i==1){
		if(PtrL){
			L = PtrL;
			PtrL = PtrL->Next;
			free(L);
			return PtrL;
		}
		else{
			return NULL;
		}

	}
	P = FindKth(i-1,PtrL);
	L = P->Next;
	if(P==NULL||L==NULL){
		printf("结点错误\n");
		return NULL;
	}else{

		P->Next = L->Next;
		free(L);
		return PtrL;
	}	
} 
 
void Print(List L){
	List t;
	int flag = 1;
	printf("当前链表为：");
	for(t = L;t;t =t->Next){
		printf("%d  ",t->Data);
		flag = 0;
	}
	if(flag)
		printf("NULL");
	printf("\n"); 
}

int main(){
//	PtrL = MakeEmpty();
//	Print(PtrL);
	PtrL = Insert(11,1,PtrL);
	PtrL = Insert(25,1,PtrL);
	PtrL = Insert(33,2,PtrL);
	PtrL = Insert(77,3,PtrL);
	Print(PtrL);
	printf("当前链表长度为：%d\n",Length(PtrL));
	printf("此时链表中第二个结点的值是：%d\n",FindKth(2,PtrL)->Data);
	printf("查找22是否在该链表中：");
	if(Find(22,PtrL))
		printf("是！\n");
	else
		printf("否！\n");
	printf("查找33是否在该链表中：");
	if(Find(33,PtrL))
		printf("是！\n");
	else
		printf("否！\n");
	PtrL = Delete(1,PtrL);
	PtrL = Delete(3,PtrL);
	printf("----------删除后-----\n"); 
	Print(PtrL);
	return 0;
}

当前链表为：NULL
当前链表为：25  33  77  11
当前链表长度为：4
此时链表中第二个结点的值是：33
查找22是否在该链表中：否！
查找33是否在该链表中：是！
----------删除后-----
当前链表为：33  77

--------------------------------
Process exited after 0.3281 seconds with return value 0
请按任意键继续. . .

广义表(Generalized List)

广义表是线性表的推广
对于线性表而言，n个元素都是基本的单元素

广义表中，这些元素不仅可以是单元素也可以是另一个广义表

typedef struct GNode *GList
struct GNode{
	int Tag;	/*标志域：0表示结点是单元素，1表示结点是广义表*/
	union{	/*子表指针域SubList与单元素数据域Data复用，即共用存储空间*/
		ElementType Data;
		GList SubList;	
	}URegion
	GList Next;	/*指向后继结点*/
}

多重链表

双向链表不属于多重链表
- 十字链表

打卡第二天

2.2 堆栈

什么是堆栈(Stack)？

具有一定操作约束的线性表，只在一端（栈顶，Top）做插入、删除。

插入数据：入栈（Push）

删除数据：出栈（Pop）

出栈方式计算

卡特兰数：

递推关系的解为：

h(n)=C(2n,n)/(n+1) (n=0,1,2,…)

递推关系的另类解为：

h(n)=C(2n,n)-C(2n,n+1)(n=0,1,2,…)

后入先出：Last In First Out（LIFO）
- 前缀表达式：运算符号位与两个运算数之前。如，- + a * b c / d e
- 中缀表达式：运算符号位与两个运算数之间。如，a + b * c - d / e
- 后缀表达式：运算符号位于连个运算数之后。如，a b c * + d e / -
  - 后缀表达式求值策略：从左向右“扫描”，逐个处理运算数和运算符号
堆栈的抽象数据类型描述
- 类型名称：堆栈（Stack）
- 数据对象集：一个有0个或多个元素的有穷线性表
- 操作集：长度为MaxSize的堆栈S∈Stack，堆栈元素item∈ElementType
1. Stack CreateStack(int Size)：生成空堆栈，其最大长度为MaxSize
2. int IsFull(Stack S,int MaxSize)：判断堆栈S是否已满
3. void Push(Stack S,ElementType item)：将元素item压入栈内
4. int IsEmpty(Stack S)：判断堆栈S是否为空
5. ElementType Pop(Stack S)：删除并返回栈顶元素

栈的顺序存储实现

栈的顺序存储结构通常由一个一维数组和一个记录栈顶元素位置的变量组成

#include<stdio.h>
#include<malloc.h>
#define MaxSize 100
typedef int ElementType;
typedef struct SNode *Stack;
struct SNode{
	ElementType *Data;
	int Top;
};
//初始化堆栈
Stack CreateStack(Stack S){
	S = (Stack)malloc(sizeof(struct SNode));
	S->Data = (ElementType *)malloc(MaxSize*sizeof(ElementType));
	S->Top = -1;
	return S;
} 
//判断堆栈是否已满
int IsFull(Stack S){
	return (S->Top == MaxSize-1);
} 
//入栈
void Push(Stack S,ElementType X){
	if(IsFull(S)){
		printf("堆栈满\n");
		return;
	}
	S->Data[++(S->Top)] = X;
}
//判断堆栈是否为空
int IsNull(Stack S){
	return (S->Top == -1);
}
//出栈
ElementType Pop(Stack S){
	if(IsNull(S)){
		printf("堆栈为空\n");
		return;
	}
	return S->Data[(S->Top)--];
} 
int main(){
	Stack S = CreateStack(S);
	printf("1入栈\n");
	Push(S,1);
	printf("2入栈\n");
	Push(S,2);
	printf("3入栈\n");
	Push(S,3);
	printf("%d出栈\n",Pop(S));
	printf("%d出栈\n",Pop(S));
	printf("%d出栈\n",Pop(S));
	return 0;
}

1入栈
2入栈
3入栈
3出栈
2出栈
1出栈

--------------------------------
Process exited after 0.03336 seconds with return value 0
请按任意键继续. . .

栈的链式储存实现

栈的链式存储结构实际上就是一个单链表，叫做链栈。插入和删除操作只能在链栈的栈顶进行。

#include<stdio.h>
#include<malloc.h>
typedef struct SNode *Stack;
typedef int ElementType;
struct SNode{
	ElementType Data;
	Stack Next;
};
Stack S;
//初始化链栈 
Stack CreateStack(Stack S){
	S = (Stack)malloc(sizeof(struct SNode)); 
	S->Next = NULL; 
	return S;
}
//入栈 
void Push(ElementType X,Stack S){
	Stack Tmp = (Stack)malloc(sizeof(struct SNode));
	Tmp->Data = X;
	Tmp->Next = S->Next;
	S->Next = Tmp;
}
//判断堆栈是否为空 
int IsNull(Stack S){
	return (S->Next == NULL);
}
//出栈 
ElementType Pop(Stack S){
	if(IsNull(S)){
		printf("堆栈为空");
		return; 
	}
	Stack Tmp = S->Next;
	ElementType val = Tmp->Data;
	S->Next = Tmp->Next;
	free(Tmp);
	return val;
}
int main(){
	S = CreateStack(S);
	printf("1入栈\n");
	Push(1,S);
	printf("2入栈\n");
	Push(2,S);
	printf("3入栈\n");
	Push(3,S);
	printf("%d出栈\n",Pop(S));
	printf("%d出栈\n",Pop(S));
	printf("%d出栈\n",Pop(S));
	return 0;
}

1入栈
2入栈
3入栈
3出栈
2出栈
1出栈

--------------------------------
Process exited after 0.2672 seconds with return value 0
请按任意键继续. . .

中缀表达式求值

基本策略：将中缀表达式转换为后缀表达式，然后求值

中缀表达式如何转换成后缀表达式？

从头到尾读取中缀表达式的每个对象，对不同对象按不同的情况处理。
- 运算数：直接输出
- 左括号：压入堆栈
- 右括号：将栈顶的运算符弹出并输出，直到遇到左括号(出栈，不输出)
- 运算符
  - 若优先级大于栈顶运算符时，则把它压栈
  - 若优先级小于等于栈顶运算符时，将栈顶运算符弹出并输出；再比较新的栈顶运算符，直到该运算符大于栈顶运算符优先级为止，然后将该运算符压栈
- 若各对象处理完毕，则把堆栈中存留的运算符一并输出
堆栈的其他应用
- 函数调用及递归实现
- 深度优先搜索
- 回溯算法
- ……

2.3 队列

定义：具有一定操作约束的线性表
- 插入和删除操作：只能在一段插入，而在另一端删除
- 数据插入：入队列(AddQ)
- 数据深处：出队列(DeleteQ)
- 先来先服务
- 先进先出：FIFO
抽象数据类型描述
- 类型名称：队列(Queue)
- 数据对象集：一个有0个或多个元素的有穷线性表
- 操作集：长度为MaxSize的队列Q∈Queue，队列元素item∈ElementType
1. Queue CreatQueue(int MaxSize)：生成长度为MaxSize的空队列
2. int IsFullQ(Queue Q,ElementType item)：将数据元素item插入队列Q中
3. void AddQ(Queue Q,ElementType item)：将数据元素item插入队列Q中
4. int IsEmptyQ(Queue Q)：判断队列Q是否为空
5. ElementType DeleteQ(Queue Q)：将队头数据元素从队列中删除并返回

队列的顺序存储实现

#include<stdio.h>
#include<malloc.h>
#define MaxSize 100
typedef int ElementType;
typedef struct QNode *Queue;
struct QNode{
	ElementType Data[MaxSize];
	int front;
	int rear;
};
//初始化队列
Queue CreateQueue(){
	Queue Q = (Queue)malloc(sizeof(struct QNode));
	Q->front = -1;
	Q->rear = -1;
	return Q;
} 
//判断队列是否已满
int IsFull(Queue Q){
	return ((Q->rear+1)%MaxSize == Q->front);
} 
//入队
void AddQ(Queue Q,ElementType X){
	if(IsFull(Q)){
		printf("队列已满\n");
		return; 
	}
	Q->rear = (Q->rear+1)%MaxSize;
	Q->Data[Q->rear] = X;
}
//判断队列是否为空
int IsEmpty(Queue Q){
	return (Q->front == Q->rear);
} 
//出队
ElementType DeleteQ(Queue Q){
	if(IsEmpty(Q)){
		printf("队列为空\n");
		return;
	} 
	Q->front = (Q->front+1)%MaxSize;
	return Q->Data[Q->front];
}
int main(){
	Queue Q = CreateQueue();
	AddQ(Q,3);
	printf("3入队\n");
	AddQ(Q,5);
	printf("5入队\n");
	AddQ(Q,11);
	printf("11入队\n");
	printf("%d出队\n",DeleteQ(Q));
	printf("%d出队\n",DeleteQ(Q));
	return 0;
}

3入队
5入队
11入队
3出队
5出队

--------------------------------
Process exited after 0.9975 seconds with return value 0
请按任意键继续. . .

队列的顺序存储实现

#include<stdio.h>
#include<malloc.h>
typedef struct QNode *Queue;
typedef struct Node *List;
typedef int ElementType;
struct Node{
	ElementType Data;
	List Next; 
};
struct QNode{
	List rare;
	List front;
}; 
//初始化队列
Queue CreateQueue(){
	Queue Q;
	Q = (Queue)malloc(sizeof(struct QNode));
	Q->front = NULL;
	Q->rare = NULL;
	return Q;
} 
//入队
void AddQ(ElementType X,Queue Q){
	List L = (List)malloc(sizeof(struct Node));
	L->Data = X;
	if(Q->rare == NULL){
		Q->front = L;
		Q->rare = L;
		return;
	}
	Q->rare->Next = L;
	Q->rare = L;
}
//判断队列是否为空 
int IsEmpty(Queue Q){
	return (Q->front ==NULL);
} 
//出队
ElementType DeleteQ(Queue Q){
	if(IsEmpty(Q)){
		printf("队列为空\n");
		return;
	}
	List Tmp = Q->front;
	if(Q->front == Q->rare) {
		Q->front = Q->rare = NULL;
	}else{
		Q->front = Tmp->Next;
	}
	ElementType Tmp2 = Tmp->Data;
	free(Tmp);
	return Tmp2;
} 
int main(){
	Queue Q = CreateQueue();
	AddQ(1,Q);
	printf("入队1\n"); 
	AddQ(2,Q);
	printf("入队2\n"); 
	AddQ(3,Q);
	printf("入队3\n"); 
	printf("出队%d\n",DeleteQ(Q));
	printf("出队%d\n",DeleteQ(Q));
	printf("出队%d\n",DeleteQ(Q));
	DeleteQ(Q);
	return 0;
}

入队1
入队2
入队3
出队1
出队2
出队3
队列为空

--------------------------------
Process exited after 0.2437 seconds with return value 0
请按任意键继续. . .

多项式相加相乘

#include<stdio.h>
#include<malloc.h>
typedef int ElementType;
typedef struct Node *List;
struct Node{
	int coef;
	int expon;
	List link;
};
void Attach(int coef,int expon,List *rear){
	List L = (List)malloc(sizeof(struct Node));
	L->coef = coef;
	L->expon = expon;
	L->link = NULL; 
	(*rear)->link = L;
	*rear = L;
}
//读入多项式 
List CreateList(){
	int n;
	int coef,expon;
	List Front;
	List Tmp; 
	List Rear;
	scanf("%d",&n);
	Rear = (List)malloc(sizeof(struct Node));
	Rear->link = NULL;
	Tmp = Rear;
	Front = Rear;
	while(n--){
		scanf("%d%d",&coef,&expon);
		Attach(coef,expon,&Rear);
	}
	Front = Front->link;
	free(Tmp);//删除头部空结点 
	return Front; 	
} 
//多项式相加
List Add(List L1,List L2){
	List Rear = (List)malloc(sizeof(struct Node));
	Rear->link = NULL;
	List Front = Rear;
	List Tmp1 = L1;
	List Tmp2 = L2;
	while(Tmp1&&Tmp2){//判断从左到右系数依此降低 
		if(Tmp1->expon>Tmp2->expon){
			Attach(Tmp1->coef,Tmp1->expon,&Rear);
			Tmp1 = Tmp1->link;
		}else if(Tmp1->expon<Tmp2->expon){
			Attach(Tmp2->coef,Tmp2->expon,&Rear);
			Tmp2 = Tmp2->link;
		}else{
			int sum = Tmp1->coef+Tmp2->coef;
			if(sum!=0){
				Attach(sum,Tmp1->expon,&Rear);
			}
			Tmp1 = Tmp1->link;
			Tmp2 = Tmp2->link;
		}
	}
	//将剩余的依此加入 
	while(Tmp1){
		Attach(Tmp1->coef,Tmp1->expon,&Rear);
		Tmp1 = Tmp1->link;
	}
	while(Tmp2){
		Attach(Tmp2->coef,Tmp2->expon,&Rear);
		Tmp2 = Tmp2->link;
	}
	List Temp = Front;
	Front = Front->link;
	free(Temp);
	return Front;
}
List Multiply(List L1,List L2){
	//判断是否为空 
	if(!L1||!L2){
		return NULL;
	}
	List Rear = (List)malloc(sizeof(struct Node));
	Rear->link = NULL;
	List Front = Rear;
	List Tmp1 = L1;
	List Tmp2 = L2;
	List Temp;
	while(Tmp2){
		Attach(Tmp1->coef*Tmp2->coef,Tmp1->expon+Tmp2->expon,&Rear);
		Tmp2 = Tmp2->link;
	}
	Tmp1 = Tmp1->link;
	while(Tmp1){
		Tmp2 = L2;
		Rear = Front;//将Rear置为头结点 
		while(Tmp2){
			int coef = Tmp1->coef*Tmp2->coef;
			int expon = Tmp1->expon+Tmp2->expon;
			while(Rear->link&&Rear->link->expon>expon){//找出插入的位置 
				Rear = Rear->link;
			}
			if(Rear->link&&Rear->link->expon==expon){//如果指数相等 
				if(Rear->link->coef+coef){//如果系数相加不为零 
					Rear->link->coef+=coef;
				}
				else{//系数相加等于零，删除 
					Temp = Rear->link;
					Rear->link = Temp->link;
					free(Temp);
				}
			}else{//插入在链表中 
				Temp =(List)malloc(sizeof(struct Node));
				Temp->coef = coef;
				Temp->expon = expon;
				Temp->link = Rear->link;
				Rear->link = Temp;
				Rear = Rear->link;
			}
			Tmp2 = Tmp2->link;
		}
		Tmp1 = Tmp1->link;
	}
	Temp = Front;
	Front=Front->link;
	free(Temp);
	return Front;
}
void Print(List L){
	List Tmp = L;
	while(Tmp){
		printf("%d %d ",Tmp->coef,Tmp->expon);
		Tmp = Tmp->link;
	}
	printf("\n");
} 
int main(){
	List L1,L2;
	L1 = CreateList();
	L2 = CreateList();
	Print(Multiply(L1,L2));
	Print(Add(L1,L2));
}

4 3 4 -5 2 6 1 -2 0
3 5 20 -7 4 3 1
15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0

--------------------------------
Process exited after 40.26 seconds with return value 10
请按任意键继续. . .

打卡第三天

第三讲树（上）

3.1 树与树的表示

什么是树？

客观世界中许多事物存在层次关系
- 人类社会家谱
- 社会组织结构
- 图书信息管理
- ……
查找(Searching)

查找：根据某个给定的关键字K，从集合R中找出关键字与K相同的记录
- 静态查找：集合中记录是固定的
  - 没有插入和删除操作，只有查找
- 动态查找：集合中记录时动态变化的
  - 除查找，还可能发生插入和删除

静态查找

方法1：顺序查找（时间复杂度O(n)）

#include<stdio.h>
  #include<malloc.h>
#define MAXSIZE 100
  typedef int ElementType;
  typedef struct Node *List; 
  struct Node{
  	ElementType Data[MAXSIZE];
  	int length;
  };
  List CreateEmpty(){
  	List L = (List)malloc(sizeof(struct Node));
  	L->length = 0;
  	return L;
  }
  void Add(List L,ElementType X){
  	L->Data[++L->length] = X;
  }
  int SequentialSearch(List Tbl,ElementType K){
  	int i;
  	Tbl->Data[0] = K;
  	for(i=Tbl->length;Tbl->Data[i]!=K;i--);
  	return i;
  }
  int main(){
  	int n;
  	List L = CreateEmpty();
  	Add(L,1);
  	Add(L,2);
  	Add(L,3);
  	Add(L,4);
  	Add(L,5);
  	while(scanf("%d",&n)!=EOF){
  		printf("%d\n",SequentialSearch(L,n));
  	}
  }

方法2：二分查找（时间复杂度O(logn)）

前提：数据的关键字满足有序，并且连续存放（数组）

#include<stdio.h>
#include<malloc.h>
#define MAXSIZE 100
#define NotFound -1 
typedef int ElementType;
typedef struct Node *List;
struct Node{
	ElementType Data[MAXSIZE];
	int length;
}; 
List CreateEmpty(){
	List L = (List)malloc(sizeof(struct Node));
	L->length = 0;
}
void Add(List L,ElementType X){
	L->Data[L->length++] = X;
}
int BinarySearch(List Tbl,ElementType X){
	int left,mid,right;
	left = 0;
	right = Tbl->length-1;
	while(left<=right){
		mid = (left+right)/2;
		if(Tbl->Data[mid]<X){
			left = mid+1;
		} 
		else if(Tbl->Data[mid]>X){
			right = mid-1;
		}
		else{
			return mid;
		}
	}
	return NotFound;
}
int main(){
	ElementType n;
	List L = CreateEmpty();
	Add(L,5);
	Add(L,13); 
	Add(L,19); 
	Add(L,21); 
	Add(L,37); 
	Add(L,56); 
	Add(L,64); 
	Add(L,75); 
	Add(L,80); 
	Add(L,88); 
	Add(L,92);
	scanf("%d",&n);
	printf("%d",BinarySearch(L,n)+1);
	return 0;
}

88
10
--------------------------------
Process exited after 4.672 seconds with return value 0
请按任意键继续. . .

树的定义

树（Tree）：n(n≥0)个结点构成的有限集合
- 当n=0时，称为空树；
- 对于任一棵非空树(n＞0)，它具备以下性质：
  - 树中有一个称为“根（Root）”的特殊结点，用r表示
  - 其余结点可分为m(m>0)个互不相交的有限集T₁,T₂,…,T_m，其中每个集合本身又是一棵树，称为原来树的“子树（SubTree）”
  - 子树是不相交的
  - 除了根结点外，每个结点有且仅有一个父结点
  - 一棵N个结点的树有N-1条边
树的一些基本术语
1. 结点的度（Degree）结点的子树个数
2. 树的度：树的所有结点中最大的度数
3. 叶结点（Leaf）：度为0的结点
4. 父结点（Parent）：有子树的结点是其子树的根结点的父结点
5. 子结点（Child）：若A结点是B结点的父结点，则称B结点是A结点的子结点；子结点也称孩子结点
6. 兄弟结点（Sibling）：具有同一父结点的各结点彼此是兄弟结点
7. 路径和路径长度：从结点n₁到n_k的路径为一个结点序列n₁，n₂，…，n_k，n_i是n_i+1的父结点。路径所包含边的个数为路径的长度
8. 祖先结点（Ancestor）：沿树根到某一结点路径上所有结点都是这个结点的祖先结点
9. 子孙结点（Descendant）：某一结点的子树中的所有结点是这个结点的子孙
10. 结点的层次（Level）：规定根结点在1层，其他任意结点的层数是其父结点的层数加1
11. 树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度
树的表示

儿子 - 兄弟表示法（二叉树其实就是儿子-兄弟表示法的链表右移 45° 得到的结果）
- Element 存值
- FirstChild 指向第一个儿子
- NextSibling 指向下一个兄弟
Element

FirstChild NextSibiling

Element
FirstChild	NextSibiling

3.2 二叉树及存储结构

二叉树的定义及性质
- 二叉树的定义：有一个有穷的结点集合
  - 这个集合可以为空
  - 若不为空，则它是由根结点合称为其左子树T_L和右子树T_R的两个不相交的二叉树组成
  - 二叉树具体五种基本形态
    1. 空树
    2. 只有一个结点
    3. 一个结点和左子树
    4. 一个结点和右子树
    5. 一个结点和左子树和右子树
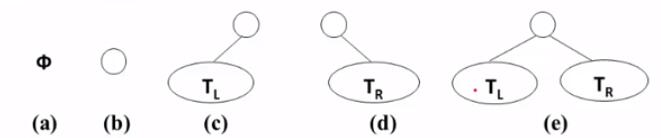
  - 二叉树的子树有左右顺序之分（一般的度为二的树没有左右顺序之分）
  - 特殊二叉树
    - 斜二叉树（Skewed Binary Tree）
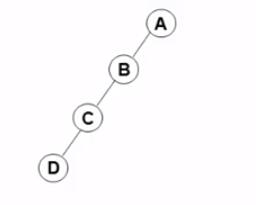
    - 完美二叉树（Perfect Binary Tree）、满二叉树（Full Binary Tree）
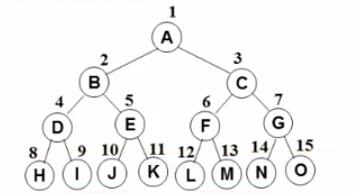
    - 完全二叉树（Complete Binary Tree)
      
      有n个结点的二叉树，对树中结点按从上至下、从左至右顺序进行编号，编号为i（1 ≤ i ≤ n）结点与满二叉树中编号为i结点在二叉树中位置相同
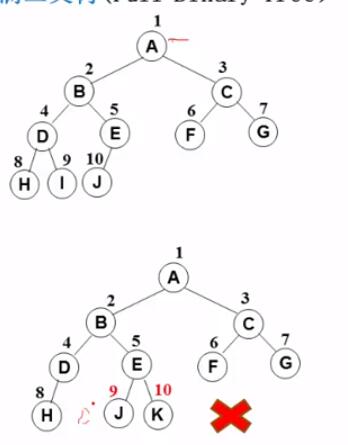
- 二叉树的几个重要性质
  - 一个二叉树第i层最大结点数为：2^i-1，i≥1
  - 深度为k的二叉树有最大结点总数为：2^k-1，k≥1
  - 对任何非空二叉树T，若n₀**表示叶结点的个数、n₂是度为2的非叶结点个数，那么两者满足关系n₀=n₂+1**
    
    推导：n₀+n₁+n₂-1=0×n₀+1×n₁+2×n₂（从下向上看总的边数等于从上向下看总的边数）
- 二叉树的抽象数据类型定义
  - 类型名称：二叉树
  - 数据对象集：一个有穷的结点集合
    
    若不为空，则由根结点和其左，其右二叉子树组成
  - 操作集：BT∈BinTree，Item∈ElementType，重要操作有：
    1. Boolean IsEmpty(BinTree BT)：判别BT是否为空
    2. void Traversal(BinTree BT)：遍历，按某顺序访问每个结点
    3. BinTree CreatBinTree()：创建一个二叉树
      
      常见的遍历方法有：
      - void PreOrderTraversal(BinTree BT)：先序—>根、左子树、右子树
      - void InOrderTraversal(BinTree BT)：中序—>左子树、根、右子树
      - void PostOrderTraversal(BinTree BT)：后序—>左子树、右子树、根
      - void LevelOrderTraversal(BinTree BT)：层次遍历，从上到下，从左到右
- 二叉树的存储结构
  1. 顺序存储结构
    
    完全二叉树：按从上至下、从左到右顺序存储n个结点的完全二叉树的结点父子关系
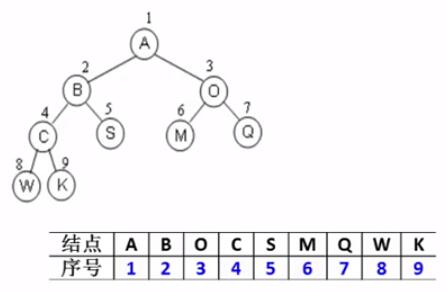
    - 非根结点（序号i＞1）的父结点的序号是 [i/2]
    - 结点（序号为i）的左孩子结点的序号是2i，（若2i≤n，否则没有左孩子）
    - 结点（序号为i）的右孩子结点的序号是2i+1，（若2i+1≤n，否则没有右孩子）
    一般二叉树：存储方式和完全二叉树一样，并符合完全二叉树特性（会造成一定的空间浪费）
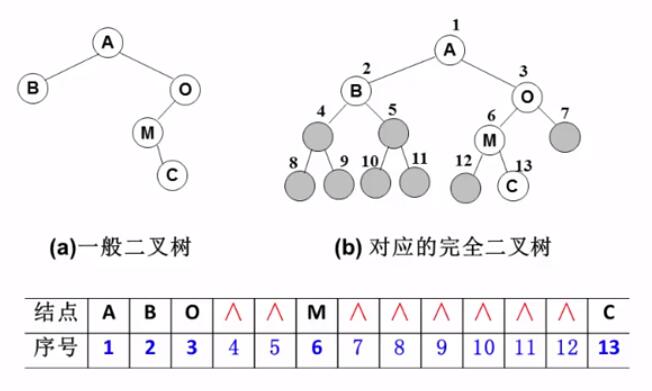
  2. 链表存储
    
    Left Data Right
    1
    2
    3
    4
    5
    6
    typedef struct TreeNode *BinTree;
    struct TreeNode{
    Element Data; // 存值
    BinTree Left; // 左儿子结点
    BinTree Right; // 右儿子结点
    };

3.3 二叉树的遍历

先序遍历

遍历过程为：

访问根结点
先序遍历其左子树

先序遍历其右子树

/*递归实现*/
void  PreOrderTraversal(BinTree BT){
	if(BT){
		printf("%d",BT->Data);  // 打印根 
		PreOrderTraversal(BT->Left);  // 进入左子树 
		PreOrderTraversal(BT->Right);  // 进入右子树 
	}
}
/*非递归实现*/
void PreOrderTraversal(BinTree BT){
	BinTree T = BT;
	Stack S = CreateStack();  // 创建并初始化堆栈 S
	while(T || !IsEmpty(S)){  // 当树不为空或堆栈不空 
		while(T){     
			Push(S,T);    // 压栈，第一次遇到该结点 
			printf("%d",T->Data);  // 访问结点
			T = T->Left;   // 遍历左子树 
		}
		if(!IsEmpty(S)){  // 当堆栈不空 
			T = Pop(S);    // 出栈，第二次遇到该结点 
			T = T->Right;  // 访问右结点 
		}
	} 
}

中序遍历

递归过程：

中序遍历其左子树
访问根结点

中序遍历其右子树

/*递归实现*/
void InOrderTraversal(BinTree BT){
	if(BT){
		InOrderTraversal(BT->Left);  // 进入左子树 
		printf("%d",BT->Data);  // 打印根 
		InOrderTraversal(BT->Right);  // 进入右子树 
	} 
}
/*非递归实现*/
void InOrderTraversal(BinTree BT){
	BinTree T = BT;
	Stack S = CreateStack();  // 创建并初始化堆栈 S
	while(T || !IsEmpty(S)){  // 当树不为空或堆栈不空 
		while(T){     
			Push(S,T);    // 压栈
			T = T->Left;   // 遍历左子树 
		}
		if(!IsEmpty(S)){  // 当堆栈不空 
			T = Pop(S);    // 出栈
			printf("%d",T->Data);  // 访问结点
			T = T->Right;  // 访问右结点 
		}
	} 
}

后序遍历

遍历过程

后序遍历其左子树
后序遍历其右子树

访问根节点

/*递归实现*/
void PostOrderTraversal(BinTree BT){
	if(BT){
		PostOrderTraversal(BT->Left);  // 进入左子树 
		PostOrderTraversal(BT->Right);  // 进入右子树 
		printf("%d",BT->Data);  // 打印根 
	} 
}

/*非递归实现*/
void PostOrderTraversal(BinTree BT){
	BinTree T = BT;
	Stack S = CreateStack();  // 创建并初始化堆栈 S
	vector<BinTree> v;   // 创建存储树结点的动态数组
	Push(S,T);
	while(!IsEmpty(S)){  // 当树不为空或堆栈不空 
		T = Pop(S);
		v.push_back(T);  // 出栈元素进数组
		if(T->Left)
			Push(S,T->Left);
		if(T->Right)
			Push(S,T->Right);
	}
	reverse(v.begin(),v.end());  // 逆转 
	for(int i=0;i<v.size();i++)  // 输出数组元素
		printf("%d",v[i]->Data);
}

总结

先序遍历是第一次”遇到”该结点时访问
中序遍历是第二次”遇到”该结点（此时该结点从左子树返回）时访问
后序遍历是第三次”遇到”该结点（此时该结点从右子树返回）时访问

层序遍历

二叉树遍历的核心问题：二维结构的线性化

从结点访问其左、右儿子结点
访问左儿子后，右儿子结点怎么办？
- 需要一个存储结构保存暂时不访问的结点
- 存储结构：堆栈（保存自己）、队列（保存右儿子）

队列实现：遍历从根结点开始，首先将根结点入队，然后开始执行循环：结点入队、访问该结点、其左右儿子入队

void LevelOrderTraversal(BinTree BT){
	queue<BinTree> q;   // 创建队列
	BinTree T;
	if(!BT)
		return;
	q.push(BT);  // BT 入队 
	while(!q.empty()){
		T = q.front();  // 访问队首元素 
		q.pop();  // 出队
		printf("%d",T->Data);
		if(T->Left)  // 如果存在左儿子结点
			q.push(T->Left);  // 入队
	 	if(T->Right)
	 		q.push(T->Right);
	}
}

第四讲树（中）

4.1 二叉搜索树

二叉搜索树（BST）也称二叉排序树或二叉查找树

性质：
- 非空左子树的所有键值小于其根结点的键值
- 非空右子树的所有键值大于其根结点的键值
- 左、右子树都是二叉搜索树

特别函数

Position Find( ElementType X, BinTree BST ) 从二叉搜索树BST中查找元素X，返回其所在结点的值
Position FindMin( BinTree BST ) 从二叉搜索树BST中查找并返回最小元素所在结点的值
Position FindMax( BinTree BST ) 从二叉搜索数BST中查找并返回最大元素所在结点的值
BinTree Insert( ElementType X, BinTree BST )

BinTree Delete( ElementType X, BinTree BST )

#include<stdio.h>
#include<malloc.h>
typedef int ElementType;
typedef struct Node *BinTree;
struct Node{
	ElementType Data;
	BinTree Right;
	BinTree Left;
};
BinTree Find(ElementType X,BinTree BST){
/*尾递归*/
//	if(!BST)
//		return NULL;
//	if(X>BST->Data)
//		return Find(X,BST->Right);
//	else if(X<BST->Data)
//		return Find(X,BST->Left);
//	else
//		return BST;
/*非递归循环执行的效率高*/ 
	while(BST){
		if(X>BST->Data)
			BST = BST->Right;
		else if(X<BST->Data)
			BST = BST->Left;
		else
			return BST;
	} 
	return NULL;
}
BinTree FindMin(BinTree BST){
/*尾递归*/ 
//	if(!BST)
//		return NULL;
//	else if(!BST->Left)
//		return BST;
//	else
//		Find(BST->Left);
	while(BST){
		while(BST->Left)
			BST = BST->Left;
		return BST;
	} 
	return NULL;
}
BinTree FindMax(BinTree BST){
/*尾递归*/ 
//	if(!BST)
//		return NULL;
//	else if(!BST->Right)
//		return BST;
//	else 
//		FindMax(BST->Right);
	while(BST){
		while(BST->Right)
			BST=BST->Right;
		return BST;	
	}
	return NULL;
}
BinTree Insert(ElementType X,BinTree BST){
	if(!BST){
		BST = (BinTree)malloc(sizeof(struct Node));
		BST->Data = X;
		BST->Left = BST->Right = NULL;
	}
	else{
		if(X<BST->Data)
			BST->Left = Insert(X,BST->Left);
		else if(X>BST->Data)
			BST->Right = Insert(X,BST->Right);
	}
	return BST;
}
BinTree Delete(ElementType X,BinTree BST){
	if(!BST){
		printf("元素未找到");
	}
	else{
		if(X>BST->Data){
			BST->Left = Delete(X,BST->Left);
		}
		else if(X<BST->Data){
			BST->Right = Delete(X,BST->Right);
		} 
		else{
			BinTree Tmp;
			Tmp = BST;
			if(BST->Left&&BST->Right){
				Tmp = FindMin(BST->Right);
				BST->Data = Tmp->Data;
				BST->Right = Delete(BST->Data,BST->Right);
			}
			else{
				if(!BST->Left){
					BST = BST->Right; 
				} 
				else if(!BST->Right){
					BST = BST->Left;
				}
				free(Tmp);
			} 
		}
	}
	return BST;
}
void  InOrderTraversal(BinTree BT){
	if(BT){
		InOrderTraversal(BT->Left);  // 进入左子树 
		printf("%d\n",BT->Data);  // 打印根 
		InOrderTraversal(BT->Right);  // 进入右子树 
	}
}
int main(){
	BinTree BST = NULL;
	BST = Insert(5,BST); 
	BST = Insert(7,BST); 
	BST = Insert(3,BST); 
	BST = Insert(1,BST); 
	BST = Insert(2,BST); 
	BST = Insert(4,BST); 
	BST = Insert(6,BST); 
	BST = Insert(8,BST); 
	BST = Insert(9,BST); 
	/*
			    5
			   /\
			  3  7
             /\	 /\
            1 4 6  8
			\      \
			 2      9
	*/
	printf("中序遍历的结果是：\n"); 
	InOrderTraversal(BST);
	printf("查找最小值是：%d\n",FindMin(BST)->Data);
	printf("查找最大值是：%d\n",FindMax(BST)->Data);
	printf("查找值为3的结点左子树结点值为：%d\n",Find(3,BST)->Left->Data);
	printf("查找值为7的结点右子树结点值为：%d\n",Find(7,BST)->Right->Data);
	printf("删除值为5的结点\n");
	Delete(5,BST);
	/*
			    6
			   /\
			  3  7
             /\	  \
            1 4    8
			\      \
			 2      9
	*/
	printf("中序遍历的结果是：\n"); 
	InOrderTraversal(BST);
	return 0;
}

4.2 平衡二叉树

“平衡因子（Balance Factor，简称BF）”：**BF(T) = h_L-h_R**，其中h_L和h_R分别为T的左、右子树的高度

平衡二叉树（Balanced Binary Tree）（AVL树）：空树，或者任意结点左、右子树高度差的绝对值不超过1，即**|BF(T)|≤1**

设n_h高度为h的平衡二叉树的最少结点数。结点数最少时：n_h = n_h-1+n_h-2+1 => n_h = F_h+2-1(h≥0) => *F_i ≈ 1/ 5^½[(1+1/ 5^½)/2]ⁱ** => h = O(logn)

平衡二叉树的调整
- 遵循原则
从离插入结点最近的结点调整

RR单旋

当”插入结点”(BR)是”被破坏平衡结点”(A)右子树的右子树时，即 RR 插入时，采用 RR 旋转调整

AVLTree RRRotation(AVLTree A){
	AVLTree B = A->right;   // B 为 A 的右子树  
	A->right = B->left;    // B 的左子树挂在 A 的右子树上 
	B->left = A;   //  A 挂在 B 的左子树上 
	return B;  // 此时 B 为根结点了   
}

LL单旋

当”插入结点”(BL)是”被破坏平衡结点”(A)左子树的左子树时，即 LL 插入，采用 RR 旋转调整

AVLTree LLRotation(AVLTree A){
	// 此时根节点是 A 
	AVLTree B = A->left;  // B 为 A 的左子树  
	A->left = B->right;   // B 的右子树挂在 A 的左子树上 
	B->right = A;     //  A 挂在 B 的右子树上 
	return B;  // 此时 B 为根结点了 
}

LR双旋
- 当”插入结点”(CL 或者 CR)是”被破坏平衡结点”(A)左子树的右子树时，即 LR 插入，采用 LR 旋转调整
  1
  2
  3
  4
  5
  6
  AVLTree LRRotation(AVLTree A){
  // 先 RR 单旋
  A->left = RRRotation(A->left);
  // 再 LL 单旋
  return LLRotation(A);
  }
RL双旋
- 当”插入结点”(CL 或者 CR)是”被破坏平衡结点”(A)右子树的左子树时，即 RL 插入，采用 RL 旋转调整
  1
  2
  3
  4
  5
  6
  AVLTree RLRotation(AVLTree A){
  // 先 LL 单旋
  A->right = LLRotation(A->right);
  // 再 RR 单旋
  return RRRotation(A);
  }

第五讲树（下）

5.1 堆

优先队列（Priority Queue）：特殊的“队列”，取出元素的顺序是依照元素的优先权（关键字）大小，而不是元素进入队列的先后顺序

实现方式：
- 数组
- 链表
- 有序数组
- 有序链表

堆（优先队列的完全二叉树表示）

堆的两个特性
- 结构性：用数组表示的完全二叉树
- 有序性：任意结点的关键字是其子树所有结点的最大值（或最小值）
  - “最大堆（MaxHeap）”，也称“大顶堆”：最大值
  - “最小堆（MinHeap）”，也称“小顶堆”：最小值
堆的抽象数据类型描述
- 数据名称：最大堆（MaxHeap）
- 数据对象集：完全二叉树，每个结点的元素值不小于其子结点的元素值
- 操作集：最大堆 H ∈ MaxHeap，元素 item ∈ ElementType
- 主要操作有：
  - MaxHeap Create(int MaxSize)：创建一个空的最大堆
  - Boolean IsFull(MaxHeap H)：判断最大堆 H 是否已满
  - Boolean Insert(MaxHeap H,ElementType item)：将元素 item 插入最大堆 H
  - Boolean IsEmpty(MaxHeap H)：判断最大堆 H 是否为空
  - ElementType DeleteMax(MaxHeap H)：返回 H 中最大元素（高优先级）

插入
插入数组最后一个位置，再从下往上找合适地方
删除
删除根结点，将数组最后一个位置的数取到根结点，从上往下找合适地方

#include<stdio.h>
#include<malloc.h>
#define MaxData 100000
#define ERROR -1
typedef int ElementType;
typedef struct HeapStruct *MaxHeap;
struct HeapStruct{
	ElementType *Elements;   // 存储堆元素的数组 
	int Size;      // 堆的当前元素个数 
	int Capacity;  // 堆的最大容量 
};

MaxHeap Create(int MaxSize);  // 建堆 
bool IsFull(MaxHeap H);    // 判断堆是否满
bool Insert(MaxHeap H,ElementType item);   // 插入元素
bool IsEmpty(MaxHeap H);    //  判断堆是否为空
ElementType DeleteMax(MaxHeap H);  // 删除并返回堆中最大元素
void LevelOrderTraversal(MaxHeap H);  // 层序遍历 

// 建堆 
MaxHeap Create(int MaxSize){
	MaxHeap H = (MaxHeap)malloc(sizeof(struct HeapStruct));
	// Elements[0] 作为哨兵，堆元素从  Elements[1] 开始存放 
	H->Elements = (ElementType *)malloc((MaxSize+1) * sizeof(ElementType));
	H->Size = 0;
	H->Capacity = MaxSize;
	// "哨兵"大于堆中所有可能的值 
	H->Elements[0] = MaxData;
	return H;
} 

// 插入，从完全二叉树的最后一个位置插入 
bool Insert(MaxHeap H,ElementType item){
	if(IsFull(H)){
		printf("堆已满，无法插入！\n");
		return false;
	}
	int i = ++H->Size;  // 指向堆中最后一个位置 
	for(;H->Elements[i/2] < item;i/=2)    // 向上找比 item 大的结点 
		H->Elements[i] = H->Elements[i/2];  //  向下赋值 
	H->Elements[i] = item;  // 找到了，把 item 值放进去 
	return true;
}

// 删除，从根结点删除 
ElementType DeleteMax(MaxHeap H){
	int parent,child;
	ElementType Max,tmp;
	if(IsEmpty(H)){
		printf("堆为空，无法删除！\n");
		return ERROR;
	}
	Max = H->Elements[1];  // 拿到最大值
	tmp = H->Elements[H->Size--];  // 拿到完全二叉树最后一个值 
	// 判别条件：parent 是否有左孩子结点 
	for(parent=1;parent*2<=H->Size;parent=child){
		// 左右孩子结点中找较大的值 
		child = 2 * parent;  // 左孩子结点 
		// child!=H->Size 表示 child 不为当前最后一个结点，即 parent 有右孩子结点 
		if((child!=H->Size) &&(H->Elements[child] < H->Elements[child+1]))
			child++;  
		// 给 tmp 找个合适的位置 
		// 如果当前左右孩子结点比 tmp 都小，说明 tmp 位置已经合适 
		if(H->Elements[child] <= tmp)
			break;
		else    // 否则把较大的孩子结点提上来，自己继续下去找 
			H->Elements[parent] = H->Elements[child];
	}
	H->Elements[parent] = tmp;  // 在合适的位置把 tmp 放进去 
	return Max;
} 

// 判断是否已经满 
bool IsFull(MaxHeap H){
	return (H->Size == H->Capacity);
}

// 判断是否为空
bool IsEmpty(MaxHeap H){
	return !H->Size;
}

// 层序遍历
void LevelOrderTraversal(MaxHeap H){
	int i;
	printf("层序遍历的结果是：");
	for(i = 1;i<=H->Size;i++){
		printf("%d ",H->Elements[i]);
	} 
	printf("\n"); 
} 

int main(){
	MaxHeap H;
	int MaxSize = 100;
	H = Create(MaxSize);
	Insert(H,55);
	Insert(H,66);
	Insert(H,44);
	Insert(H,33);
	Insert(H,11);
	Insert(H,22);
	Insert(H,88);
	Insert(H,99);
	/*
		 99
		/  \
	   88  66
	  / \  / \
	 55 11 22 44
	/ 
   33	  
	*/
	LevelOrderTraversal(H);
	DeleteMax(H);
	LevelOrderTraversal(H);
	DeleteMax(H);
	LevelOrderTraversal(H);
	DeleteMax(H);
	LevelOrderTraversal(H);
	DeleteMax(H);
	LevelOrderTraversal(H);
	return 0;
}

最小堆的建立
不是初始化堆啦！
堆的建立：将已经存在的 N 个元素按最小堆的要求存放在一个一维数组中
注意
对于一组相同数据，插入建堆和调整建堆建出来的堆也许不一样
插入建堆
通过插入，将 N 个元素一个一个相继插入到一个初始为空的堆中去，其时间代价最大是 O ( N l o g N ) O(N logN)O(NlogN)（每次插入是 logN，总共 N 次）

#include<iostream>
#include<malloc.h>
const int MinData = -100000;  // 哨兵值
const int MaxSize = 1005;   // 最大个数 
using namespace std;
typedef struct HeapStruct *Heap;
struct HeapStruct{
	int *data;   // 存值的数组 
	int size;   // 当前元素个数 
	int capacity;  // 最大容量 
};

// 初始化堆
#include<iostream>
#include<malloc.h>
const int MinData = -100000;  // 哨兵值
const int MaxSize = 1005;   // 最大个数 
using namespace std;
typedef struct HeapStruct *Heap;
struct HeapStruct{
	int *data;   // 存值的数组 
	int size;   // 当前元素个数 
	int capacity;  // 最大容量 
};

// 初始化堆
Heap Create(){
	Heap H;
	H = (Heap)malloc(sizeof(struct HeapStruct));
	H->data = (int *)malloc(sizeof(int) * (MaxSize+1));
	H->size = 0;
	H->capacity = MaxSize;
	H->data[0] = MinData;
	return H;
} 

// 插入
void Insert(Heap H,int x){
	int i = ++H->size;  // 指向数组最后一个 
	for(;H->data[i/2]>x;i/=2)
		H->data[i] = H->data[i/2];
	H->data[i] = x;
} 

// 遍历 
void bl(Heap H){
	for(int i=1;i<=H->size;i++)
		cout<<H->data[i]<<" ";
}

int main(){
	Heap H;
	H = Create();
	int n;
	cin>>n;
	for(int i=0;i<n;i++){
		int t;
		cin>>t;
		Insert(H,t);
	}
	bl(H);
	return 0;
}

调整建堆
将 N 个元素直接按顺序存入，再调整各结点的位置（简单说来，对于从最后一个有孩子结点的结点来说，其本身结点和孩子结点共同构成”子最小堆”，借助前面删除的想法，对每个”子最小堆”排序，当排序完成，整个最小堆也建立成功），时间代价是 O ( n )

#include<iostream>
#include<malloc.h>
const int MinData = -100000;  // 哨兵值
const int MaxSize = 1005;   // 最大个数 
using namespace std;
typedef struct HeapStruct *Heap;
struct HeapStruct{
	int *data;   // 存值的数组 
	int size;   // 当前元素个数 
	int capacity;  // 最大容量 
};

// 初始化堆
Heap Create(){
	Heap H;
	H = (Heap)malloc(sizeof(struct HeapStruct));
	H->data = (int *)malloc(sizeof(int) * (MaxSize+1));
	H->size = 0;
	H->capacity = MaxSize;
	H->data[0] = MinData;
	return H;
} 

// 排序，类似堆的"删除操作" 
void sort(Heap H,int i){
	int child,parent;
	int tmp = H->data[i];  // 拿到当前"根结点的值" 
	for(parent = i;parent*2<=H->size;parent = child){
		child = 2 * parent;
		if((child!=H->size) && (H->data[child+1] < H->data[child]))
			child++;
		if(H->data[child] >= tmp)
			break;
		else
			H->data[parent] = H->data[child]; 
	}
	H->data[parent] = tmp;
}
// 调整
void adjust(Heap H){
	int i= H->size/2;
	for(;i>0;i--){
		// 以每个有孩子结点的结点作为根结点，对其子树进行堆排序 
		sort(H,i);
	}
} 

// 遍历 
void bl(Heap H){
	for(int i=1;i<=H->size;i++){
		cout<<H->data[i]<<" ";
	}
	cout<<endl;
}

int main(){
	Heap H;
	H = Create();
	int n;
	cin>>n;
	for(int i=0;i<n;i++)
		cin>>H->data[++H->size];
	adjust(H);
	bl(H); 
	return 0;
}

数据结构复习（C语言） 中国大学慕课（浙大：陈越、何钦铭教授）

第一讲 基本概念